√1000以上 2次関数 最大最小 問題 807912
2次関数の最大値mの最小値 数学i ２次関数 Youtube
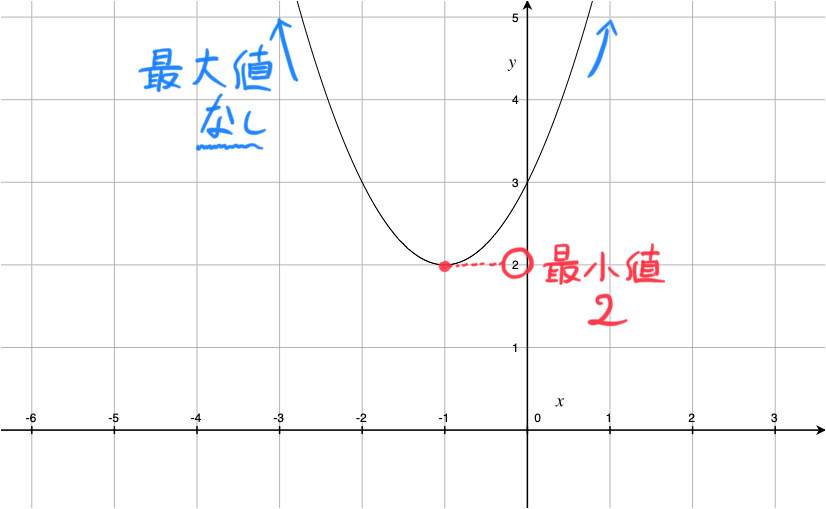
2次関数のセンター試験問題 (1) y＝2 (x－2) 2 －4 図のように谷形のグラフになるから，限りなく大きな値をとり，最大値はない x＝－2のとき最大値－4 x＝2のとき最大値－4 最大値なし (2) y＝－ (x＋3) 2 図のように頂点が (−3, 0) の山形のグラフになるから最適化問題とは関数を最小化，又は最大化する問題である．まず，以下の具体例 を紹介しよう． 例9 縦横の辺の長さの和が4 となる長方形の中で，面積が最大になるのはどのよ うな長方形か？ この問題は次のように定式化できる
2次関数 最大最小 問題
2次関数 最大最小 問題-伝説の大学入試問題（数学） スポンサーリンク 特に高校生以下の学生に数学に興味を持って欲しいと思って作成したページである。 逆に数学に恐怖を感じて萎縮しまう可能性もあるが (笑)。 良問・難問・奇問であるが故に伝説となっている、または 26 2次関数のグラフの対称移動 問題と解答 27 2次関数の最大・最小（1） 問題と解答 28 2次関数の最大・最小（2） 問題と解答 29 2次関数の最大・最小（3） 問題と解答 210 2次関数の最大・最小（4） 問題と解答 211 2次関数の最大・最小（5） 問題と
高校数学 Net
攻略 ここでは2次関数の最大・最小の問題を扱います。 この単元で特に注意することは定義域、つまり の範囲です。 問題に記されていなくても範囲が存在することがあります。 その他の2次関数に関する公式は 2次関数の攻略 と同じです。 これから何度 問題文に「実数」という単語があり，2文字の対称式が条件として与えられた2変数関数の最大最小問題の考え方と解法を説明します。 問題文に「 x, y は実数とする」なんてあっても気にしない人が多いのではないでしょうか。 また，与えられている条件式 2次関数 y = x^22ax4a5 のグラフが次の条件を満たすとき、定数aの値の範囲を求めよ。 x軸の正と負の部分で交わる。 のような問題。
・1次関数を円周上で最適化 最小化または最大化 , = 制約 2 2=1 このとき、𝑙1と円の接点が局所最大解、 𝑙3と円の接点が局所最小解になっている。 21 21 等式制約が一つの場合 𝑙1 𝑙2 𝑙3 二変数関数の最大最小：文字消去の利用 これは最も基本的なパターンです。 基本的に，動くものが2つあると扱いにくいです。 ですので，文字（変数）を1つ消去してあげて，1変数の問題として扱ってあげたいというのが文字消去の気持ちです。 等式が12 次関数の最大・最小 1 2 次関数の最大・最小 関数の値域に最大の値があるとき，その値を関数の最大値といい，最小の値があると き，その値を関数の最小値という。 2 次関数の最大・最小を求める場合は，グラフを利用して視覚的に考える。ただし，
2次関数 最大最小 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | 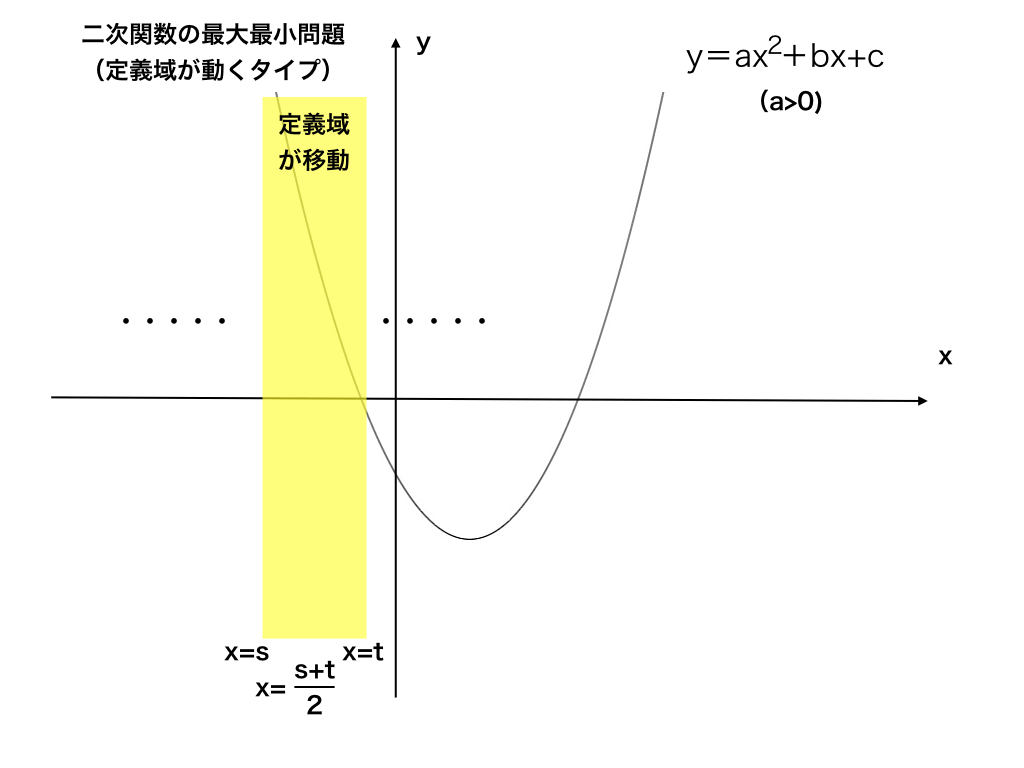 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
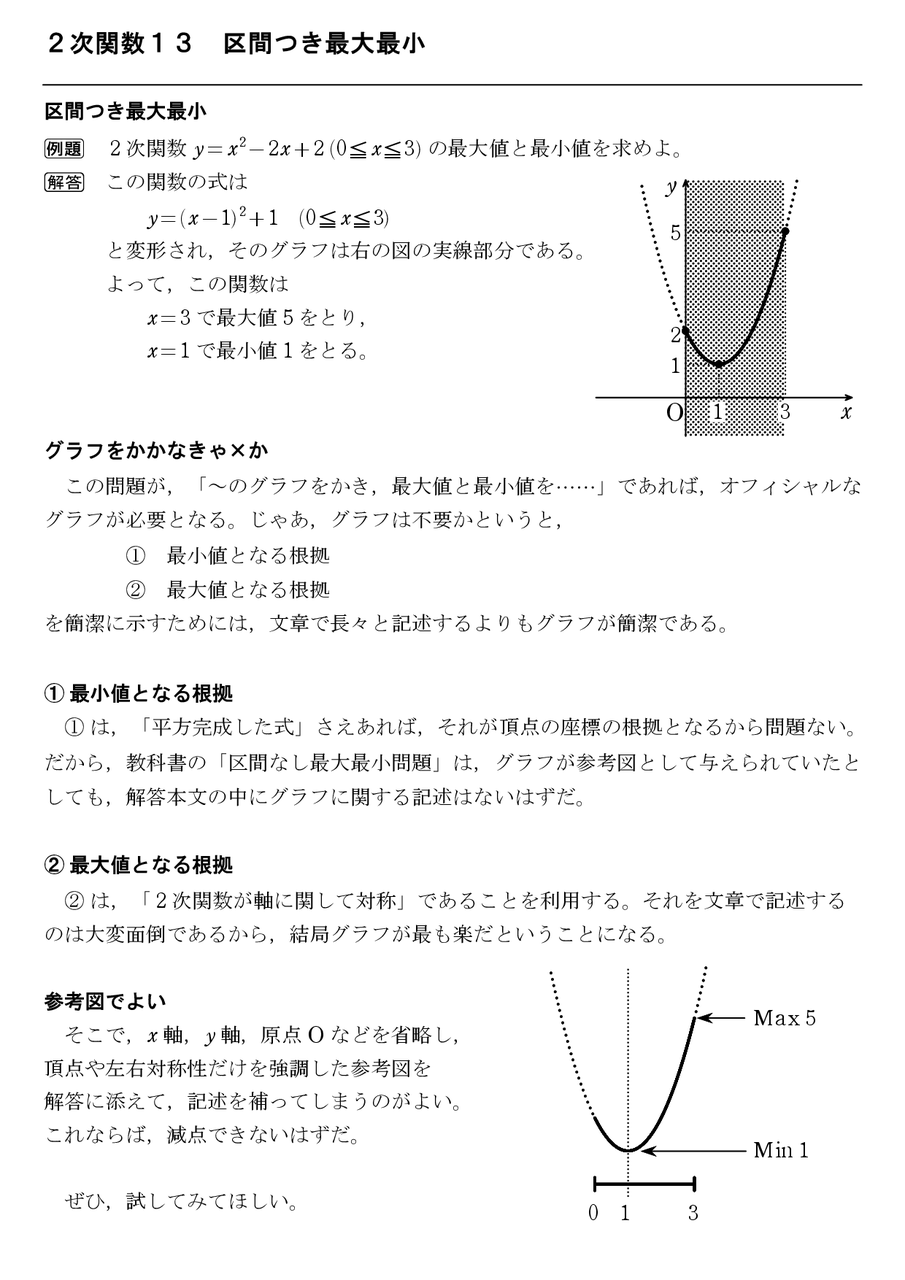 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | 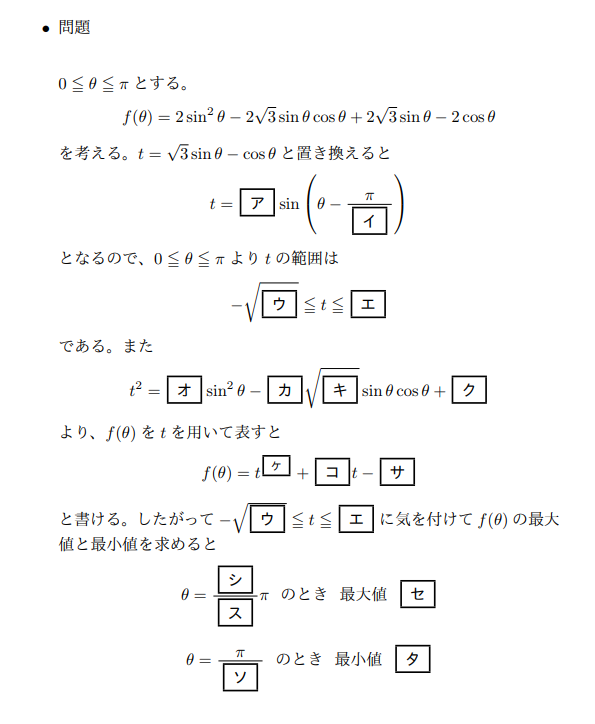 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |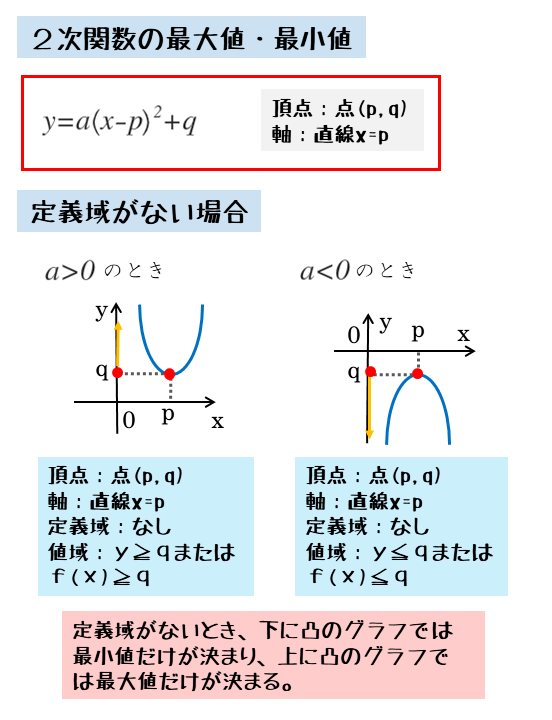
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | 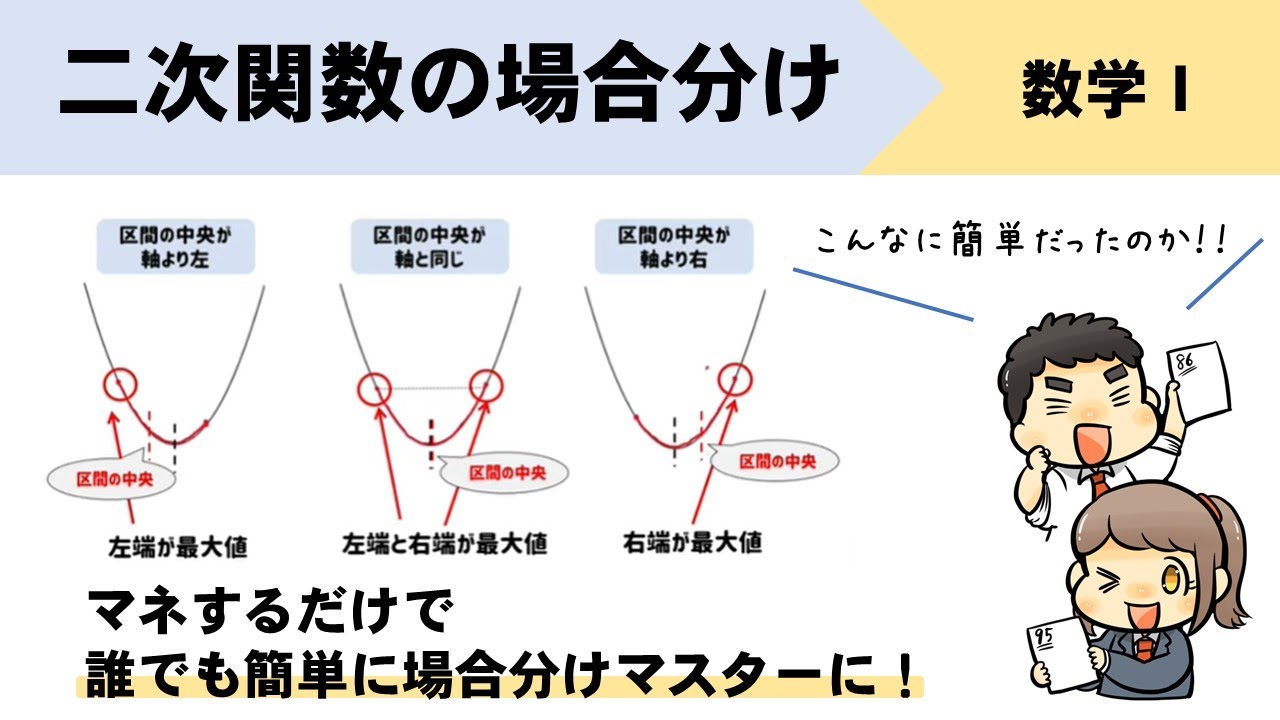 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
「2次関数 最大最小 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | 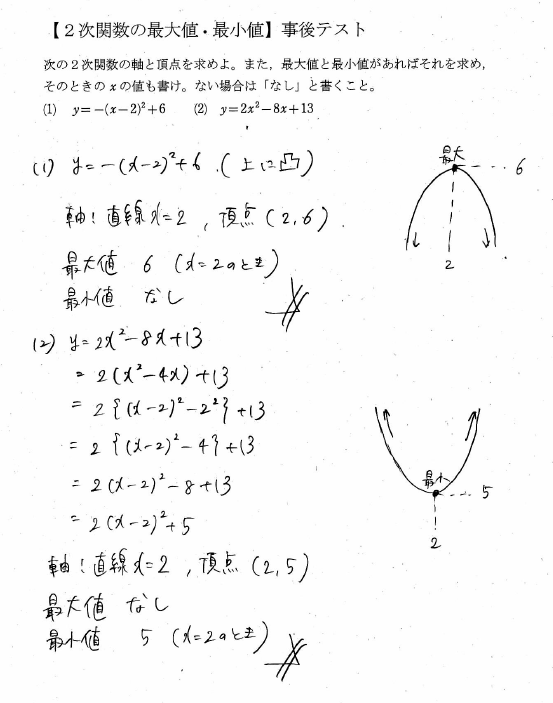 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する | ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
 ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |  ２次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する |
13 2 次関数の最大・最小 基本事項 1 2 次関数 =a( −p)2q の最大・最小 p 111 で学んだように，関数の値域における 最も大きな値を 最大値，最も小さな値を 最小値 という。2 次関数 =a( −p) q の最大・最小については，aの符 号によって，次の2 通りに分けられる。そう、そう 関数の最大値・最小値はグラフを使って解いていく ことが多いんだったんだよね。 でも、今回の問題は\(\frac{x}{x^2x1}\)と分数に変数を含んだ関数です。 こういうふうに分数に変数を含んだ関数は数学3を勉強しないと描けないよ。
コメント
コメントを投稿